一.BP算法的提出及其算法思想
神经网络主要是由三个部分组成的,分别是:1)
网络架构 2)
激活函数 3)
找出最优权重值的参数学习算法.
BP算法就是目前使用较为广泛的一种参数
学习算法.
BP(back propagation)神经网络是1986年由
Rumelhart和
McClelland为首的科学家提出的概念,是
一种按照误差逆向传播算法训练的多层前馈神经网络。
既然我们无法直接得到隐层的权值,能否先通过输出层得到输出结果和期望输出的误差来间接调整隐层的权值呢?BP算法就是采用这样的思想设计出来的算法,它的
基本思想:学习过程由
信号的正向传播(求损失)与
误差的反向传播(误差回传)两个过程组成。如图1所示为BP算法模型示意图.

图1 BP算法模型示意图
二.BP算法
2.1 BP算法的一般流程
根据BP算法的基本思想,可以得到BP算法的一般过程:
1)
正向传播FP(求损失).在这个过程中,我们根据输入的样本,给定的初始化权重值W和偏置项的值b, 计算最终输出值以及输出值与实际值之间的损失值.如果损失值不在给定的范围内则进行反向传播的过程; 否则停止W,b的更新.
2)
反向传播BP(回传误差).将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此
误差信号即作为修正各单元权值的依据。
由于BP算法是通过传递误差值δ进行更新求解权重值W和偏置项的值b, 所以BP算法也常常被叫做
δ算法.
下面我们将以三层感知器结构为例,来说明BP算法的一般计算方法(假设个隐层和输出层的激活函数为f).

图2 三层感知器结构
BP算法网络结构的示意图如图3所示.

图3 BP算法网络结构
2.2 BP算法的各层误差计算
各部分输入输出如图3所示, 下面进行各层误差计算.
1) 输出层的误差(
平方和误差,前面的1/2是为了后面的计算方便)
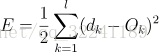
(1)
2) 展开至隐层的误差(
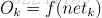
,
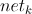
是前面的WY的输出值,带入可以得到下面的式子)

(2)
3) 输入层误差(和前面一样,将VX带入f(netj))
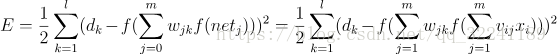
(3)
观察上式, 我们很容易看出只有(3)式和输入x有关.E有了,那么就很简单可以看出可以使用常用的
随机梯度下降法(SGD)求解.也就是求解式子中的
W和
V,使得误差E最小.



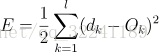 (1)
(1)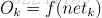 ,
,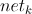 是前面的WY的输出值,带入可以得到下面的式子)
是前面的WY的输出值,带入可以得到下面的式子) (2)
(2)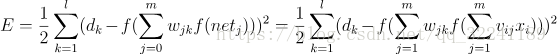 (3)
(3)